How Can I Use Models To Add Fractions

The Fear of Fractions!

Fraction is a new concept with an entirely different notation which makes it hard for students to understand. A part of the reason why students notice information technology strenuous is also that they have only ever worked with whole numbers. So naturally, fractions seem unfamiliar to them.

The struggles and challenges with fractions are existent.

The National Assessment of Educational Progress, 2005 states that "The mathematics education literature is resounding in its findings that understanding fractions is a challenging surface area of mathematics for North American students to grasp". It's this initial fright of fractions that propels farther and makes comprehending the addition and subtraction of fractions burdensome.

This commodity volition help students empathise how to add together and subtract fractions with easy steps and visual models. Nosotros'll besides look at some tricks to simplify adding and subtracting fractions.

Read on to make sure that fractions are your kids' friends and not a foe!

What are Fractions?
Types of Fractions
Models for Representing Fractions
How to Make Calculation and Subtracting Fractions Easy
Steps to Add and Decrease Fractions
Adding/Subtracting Fractions – Common Mistakes
Teach Fractions with SplashLearn
Ofttimes Asked Questions

What are Fractions?

Fractions - dividing a whole into equals

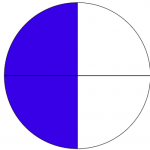
Virtually curriculums focus on fractions as shaded regions or areas, but they are beyond that. Students oftentimes see fractions equally an deed of dividing and shading parts of shapes, so they miss out on the fact that fractions are numbers between the whole numbers.

Take a close look at the ruler image below. The marking between 0 and 1 correspond numbers that are different from whole numbers. These are chosen fractions.

Fractions are numbers between whole numbers — Fractions – numbers between whole numbers

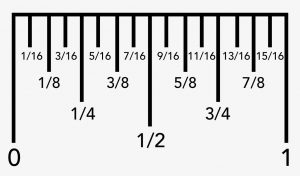
It's important to emphasize that fractions are numbers that help the states be precise and accurate with amounts. We don't e'er have 1 total kilogram or i full inch while measuring. Therefore, it becomes critical to find a way to stand for these "parts" and that is where fractions take charge.

Fractions are written as a/b where "a" is the number on the top and is called the numerator. While "b" is the number at the bottom and is chosen the denominator.

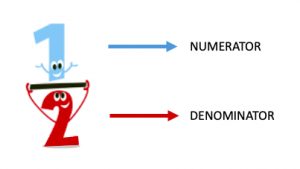
For instance: For the fraction 1/two; ane is the numerator and ii is the denominator.

Students often misfile the numerator with the denominator and vice versa. An easy mode for these confusing terms is to remember them similar – D for down and D for the denominator. So the Denominator ever goes downward!

TYPES OF FRACTIONS:

The about common types of fractions are:

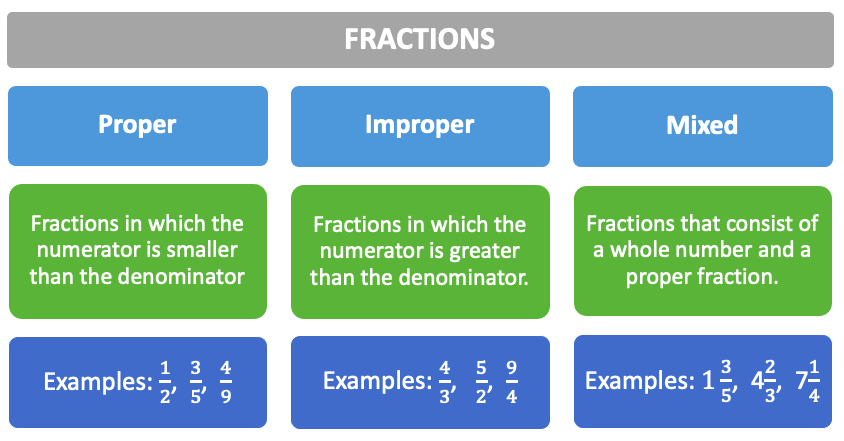
The most normally used fractions while adding and subtracting fractions are :

Like and Unlike Fractions.

Fractions with the same denominators are called Like fractions.

Example:

Like fractions have same denominators — Like fractions

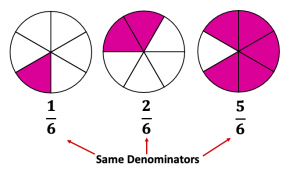
Fractions with unlike denominators are called different fractions.

Case:

Unlike fractions have different denominators — Unlike Fractions

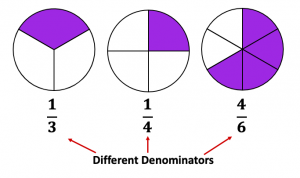
Another type of fraction that students must know before learning to add together and decrease fractions is: Equivalent Fraction

Fractions that have different numerators and denominators but are equal to the same value are called Equivalent Fractions.

Instance:

All fractions 1/2, two/4, 3/6, and 4/8 stand for the same value which is 'Half'

As fractions are similar whatsoever other numbers, they tin be represented through different models.

Models for Representing Fractions:

The most common models for representing fractions are:

a) Area Model:

In the expanse model, fractions are represented every bit parts of an expanse or a region.

Circular and rectangular fraction sets are used to develop an understanding that fractions are parts of a whole.

Examples of Area Model:

Area Model of Representing Fractions — Area Model

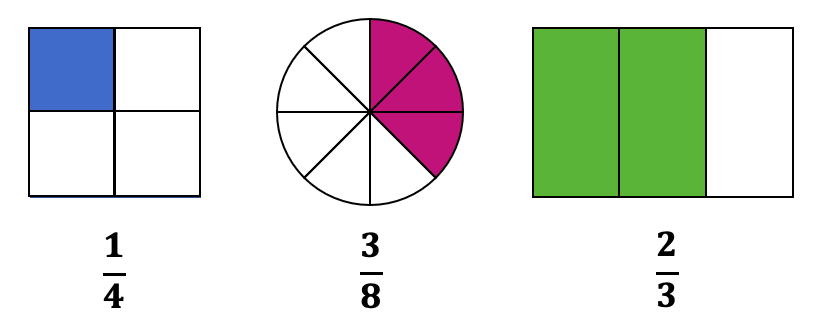
b) Linear Model:

In the linear model, fractions are considered as lengths instead of areas. The number line is an important linear model for students to grasp fractions as numbers.

The linear model for the fraction ¾ will exist:

Linear Model of Representing Fractions — Linear Model

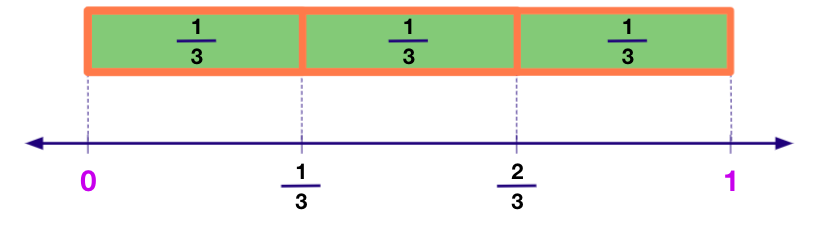
c) Discrete Model:

In the discrete model, the whole is understood to be a set of discrete objects. Subsets of this whole make up the fractional parts.

For example half of the form, i/iii of a tray of eggs. Counters, marbles, cubes or any other set of objects that tin can be counted can be used every bit a manipulative to model fractions.

Discrete Model of Representing Fractions

How to Brand Adding and Subtracting Fractions Like shooting fish in a barrel?

Doing fractions > Learning fractions

The first and foremost thing that students need to do whilst learning to add and subtract fractions is understanding fractions improve. They need to practice fractions to make connections to the real world, i.e, they need to fold papers, cut parts, color shapes, etc.

One major challenge with fractions is that information technology's not always concrete. We showtime teaching fractions through visuals merely when information technology comes to operations with fractions we switch to rules and procedures for the same. Rote memorization of the steps leads to more confusion.

In fraction addition, we add together the numerators but not the denominators. Just in fraction multiplication, we multiply the denominators as well equally the numerators. This puzzles the students fifty-fifty more than.

It'due south best advised to apply visual models to show the addition of fractions which will help students sympathize the steps rather than mugging the steps without conceptual clarity.

Activity Proposition:

To add i/8 and 3/8, take a pizza carved in viii slices

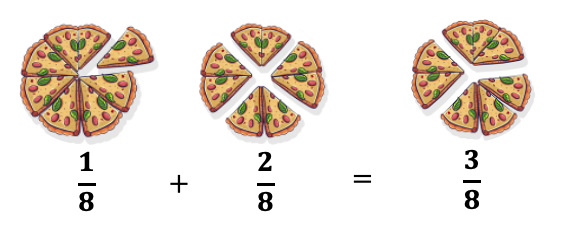
⅛ is ane slice carved out of the total eight slices,

And two/8 are ii slices out carved of the total viii slices,

Now if we add or put together both the fractions/pizza slices, we get 3 slices of the eight pizza slices which imply 3/viii.

Concrete -> Contextual -> Computational

Concrete learning to contextual learning to computational learning

To introduce a new and tricky concept like fractions, it is critical to provide students with ample opportunities to concretely absorb it. This ways immersing students in experiences similar newspaper cut, newspaper folding, drawing, paper pizzas, apples, chocolate bars, etc. Only past using such experiences will they be able to run across, touch, and feel the concept of fractions and brand their own discoveries.

Using concrete method to understand fractions

Once students get plenty of this concrete exposure, they would showtime making connections between these objects and the real world.

A lot of time should be spent creating, exploring, folding, and visualizing fractions before moving them to partial problems involving bare numbers.

For case: Before request ¼ of 20 =? , we can present a real-world scenario like this:

"Ron had twenty dollars. He spent ¼ of information technology. How much money is he left with?"

This will aid even a student with little understanding of fractions to start making connections.

Testify them "WHY" the rules work

If the notion of fractions equally numbers is developed well then it is easier to understand operations on fractions too. Just like we add and subtract numbers, fractions too tin can exist added and subtracted. It is of import to emphasize conceptual understanding along with the procedural knowledge of the steps.

For instance:

We know, 1 apple + 1 apple = 2 apples

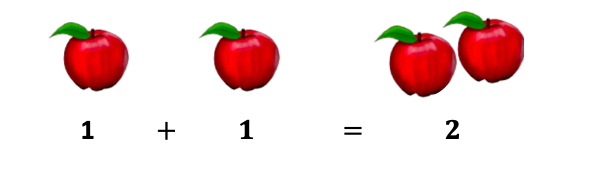
Similarly, we can add fractions likewise.

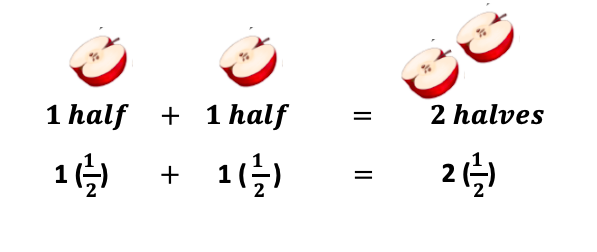
We likewise know two apples + three apples = 5 apples

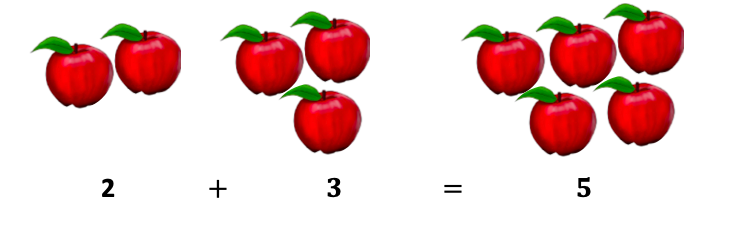
Similarly, nosotros tin can add fractions too:

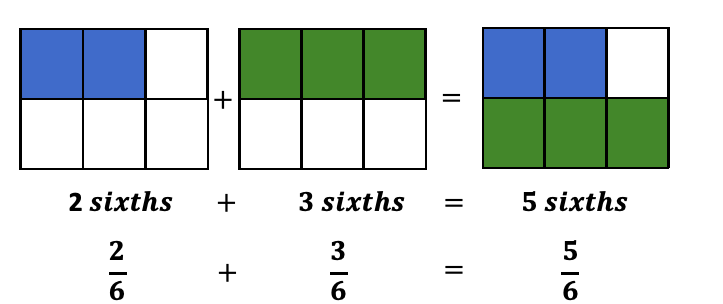
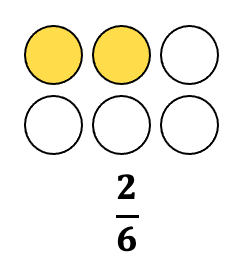
To know the sum of 2/half-dozen and 3/vi; consider information technology as two 1-sixths and iii one-sixths which will add up to five one-sixths simply like we add numbers.

Now allow's take a subtraction example:

Nosotros know v apples – 2 apples = 3 apples

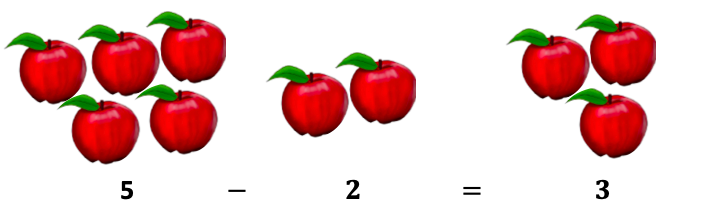
On like lines, nosotros can subtract fractions also:

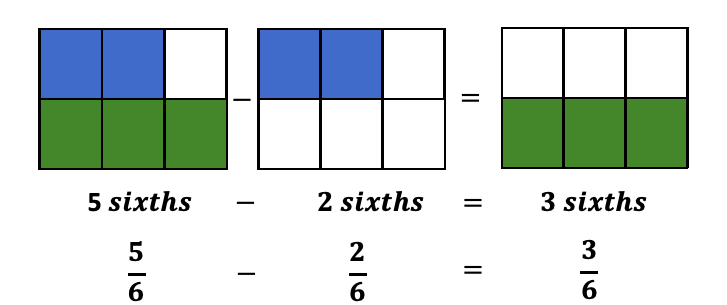
In the case of "like fractions," nosotros can just add/subtract the numerators and keep the denominator the same. But we can't add unlike fractions as we add like fractions.

The reason behind this is very simple.

Just similar we tin can't add together 2 apples and 3 oranges and say the sum is 5 applonges, nosotros can't add together fractions with dissimilar denominators. It is, thus, of import to get-go define addition as the combination of two or more like-unit quantities. Similarly, subtraction is taking away like-unit quantities.

And then, how exercise we add together/subtract dissimilar fractions? Permit'southward wait into that side by side!

STEPS TO ADD AND SUBTRACT FRACTIONS

Now, permit's expect at the steps we can follow to add or decrease fractions:

Step i: Make denominators the same

Step two: Add together or Subtract the numerators (keeping the denominator the same)

Stride 3: Simplify the fraction

To add or subtract dissimilar fractions, the first step is to brand denominators the same so that numerators can be added only like we do for like fractions.

Stride ane: Same DENOMINATORS

How do we make denominators the same?

In the instance of like fractions, the denominators will already be the same, so you can skip Step 1 and move to Step 2.

For Unlike fractions, there are 2 possibilities:

i) If ane denominator is a multiple of the other denominator

Case: ½ + ¾

Making denominators same - like fractions

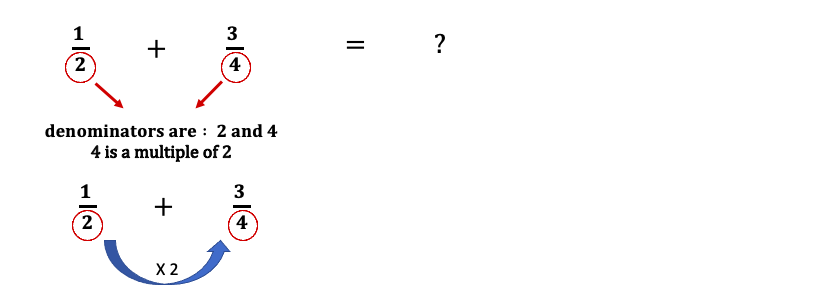
In this case – 4 is a multiple of two. We can multiply two past two to brand it iv and equally a result, the denominators volition become the same. So, the larger number becomes the common denominator.

Making the denominator same - like fractions

Applying :

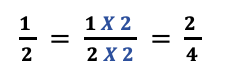
And then the problem now becomes:

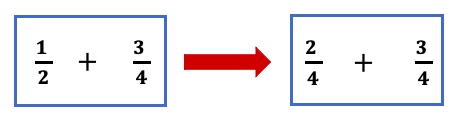
If one denominator is a multiple of the other, we tin can multiply the smaller denominator by a number (say g) that creates the larger denominator. Then the larger denominator becomes the common denominator.

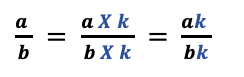
2) If both the denominators take no common factor

Case: ¼ + ⅗

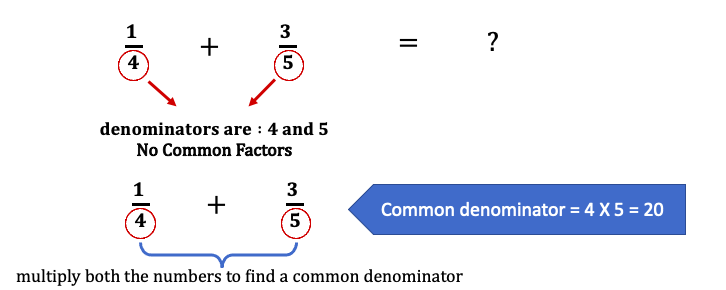
In this instance, iv and five have no mutual factors. Nosotros can only multiply the denominators to get a mutual denominator.

four Ten 5 = 20 so xx is the mutual denominator for both the fractions.

If there is no mutual factor to both the denominators then you multiply both the denominators to become the mutual denominator.

Let's see how we will go twenty as a common denominator for both the fractions:

If there is no common factor in the denominator

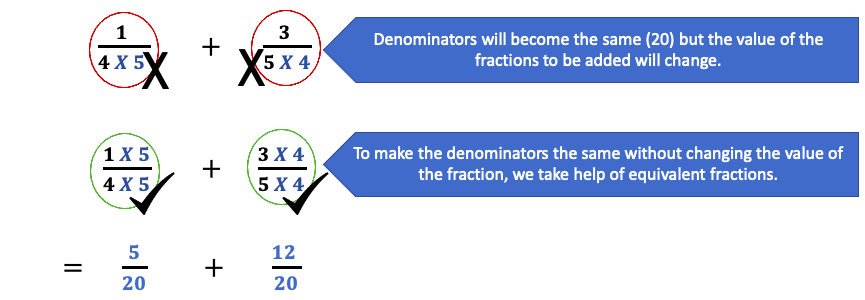
If we multiply the denominator, we have to multiply the numerator also to get an equivalent fraction.

And so the trouble now becomes:

Result with no common factor in denominator

STEP 2: Add together/SUBTRACT NUMERATORS

This pace is pretty simple and very straightforward. We have to add/subtract the numerators and the consequence of their sum/departure is the new numerator. The common denominator (as discussed in Pace ane) remains the aforementioned.

Let's have our previous examples and continue from there:

½ + ¾

After making the denominators the same, this problem looks similar this:

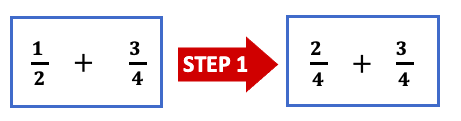
Now, nosotros demand to add the ii numerators together (2+three =5) to get the new numerator while the denominator(4) remains the aforementioned.

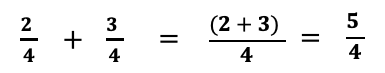
And then the respond will exist five/4.

¼ + ⅗.

After making the denominators the same, this problem looks like this:

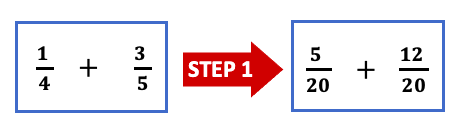
Now, we demand to add the numerators together (v + 12 = 17) to get the new numerator while the denominator(20) remains the same.

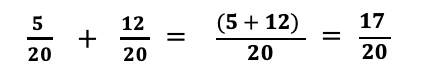
Example21addsubtractnumerators | SplashLearn

So the reply will be 17/twenty.

Step 3: SIMPLIFY THE FRACTION

The answers we have derived above are correct, just we may simplify the fraction further till at that place are no common factors in the numerator and the denominator other than one.

The fraction can be reduced to its simplified form by removing the common factors.

Let's continue with our previous examples:

And,

In the higher up cases – 5/4 and 17/20 are already simplified fractions as the numerator and the denominator take no common factors.

Let's have some examples of fractions that tin can be simplified:

four/12 is not simplified.

four is a common factor in both the numerator and the denominator so information technology can exist reduced to its simplified course as follows:

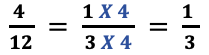
Please note: Nosotros will non be taking up mixed numbers as a separate case because these are likewise fractions written in the dissimilar (mixed) grade.

Let's summarize these steps by taking 1 example of improver and subtraction each.

Time to practice all iii steps together!

Addition Problem: 3/4 + ane/12

Footstep ane: Make the denominators the same

Denominators are 4 and 12. 12 is a multiple of four so the mutual denominator will be 12.

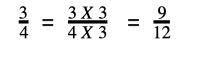
Footstep 2: Add/Subtract the numerators (keeping the denominator every bit same)

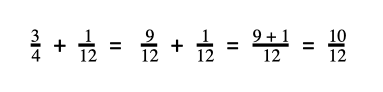
Step iii: Simplify the fraction

To simplify x/12, the mutual factor is 2

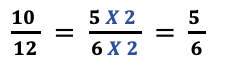
Then 10/12= 5/half dozen (in simplified form)

Hence, 3/four + 1/12= v/half dozen

Now let's wait at a subtraction problem:

Case: 2/five – 1/3

Step 1: Make the denominators the same

Common denominator will be 3 ten five = xv

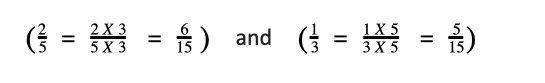
Step 2: Add/Subtract the numerators (keeping the denominator the same)

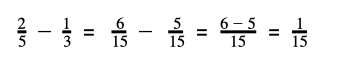
Step 3: Simplify the fraction

i/xv is in its simplified form already as 1 and 15 accept no mutual factors.

The Butterfly Method

A very interesting and useful method to quickly add/subtract fractions is the butterfly method.

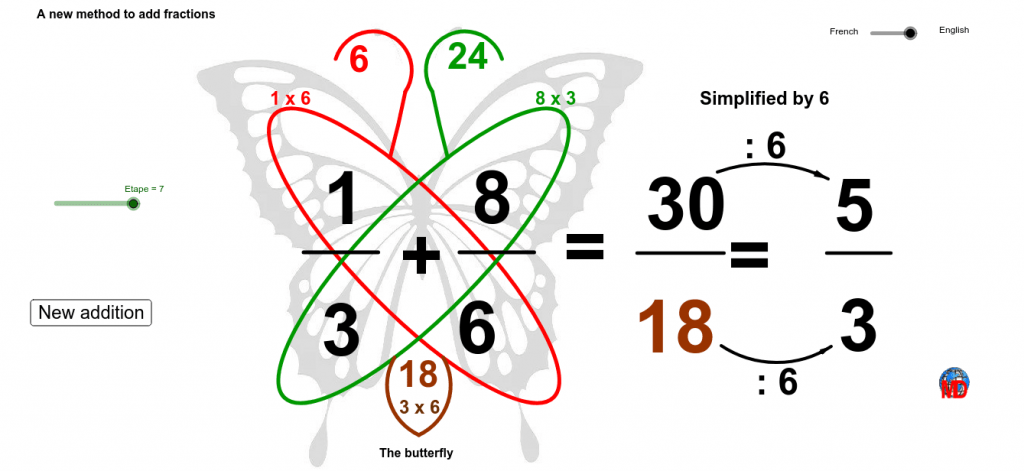
Butterfly method to add/subtract fractions — Source

In this method, nosotros draw the butterfly wings to imply which two numbers are to be multiplied together. We and so go on to write the result in the respective antenna. The denominators are multiplied and the result of that is written below in the abdomen.

In the end, we simply add/subtract the antenna and write it over the abdomen to get the result.

Adding/Subtracting Fractions – Mutual Mistakes

Teachers demand to ensure that students are taken gradually from the physical to the contextual to computational level.

Students demand to exist given a lot of examples to aid them get over some of the mutual mistakes and misconceptions:

i. Adding/subtracting numerators and denominators

One of import thing to pay close attention to while adding/subtracting fractions is the way students represent them:

The most common error in adding fractions is to add both the numerators and the denominators individually just as nosotros add whole numbers.

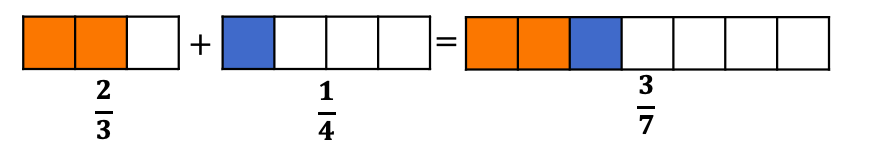
For example: When calculation 2/3 and 1/four, a common mistake is to represent each fraction as shown above and and then put them together to form 3/seven as the answer.

When students add, combine or observe the sum by putting together the wholes and both the partial parts, it only seems reasonable that they look at each fraction independently.

So, information technology is important to emphasize that fractional parts cannot exist manipulated independently from their whole.

That is why it is essential to have a mutual denominator. In the case of a mutual denominator, the fractions can be interpreted on the same diagram and combined. Let'south wait at this aforementioned instance when washed on the common whole.

In this case, the mutual denominator for two/three and 1/4 will exist 12.

Now consider the whole fabricated of 12 parts.

Now allow's detect ⅔ and ¼.

To find 2/iii first divide the whole into 3 equal parts:

Dividing a whole of 12 parts into 3 equal parts

2/3 will be 2 of these 3 equal parts:

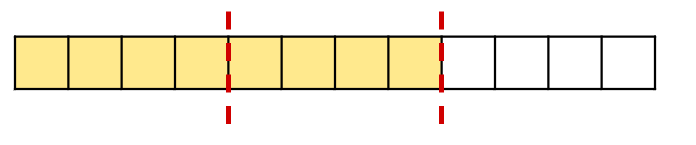
ii/iii = eight/12

Similarly, to find 1/4 we demand to split up the whole into four equal parts:

one/four volition be:

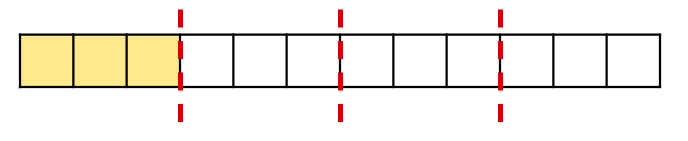
1/iv = 3/12

Now to add 2/3 and 1/iv nosotros tin can combine viii parts and iii parts whose sum equals 11 parts.

2/3 + one/four = 8/12+ three/12 = 11/12

Similarly, this aforementioned mistake is observed in subtracting fractions as well. Both the numerators and the denominators are subtracted individually just as we subtract whole numbers.

For example: 5/vi – ane/3 = (5-i)(vi-3) = four/3

Permit's discover the correct way of solving five/6 – one/three =?

In this instance, the common denominator for 5/6 and 1/iii will exist 6 (common multiple).

Now consider the whole made of 6 parts:

five/6 will exist:

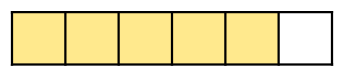
For 1/3 we carve up the whole into 3 equal parts:

dividing a whole of 6 into 3 equal parts

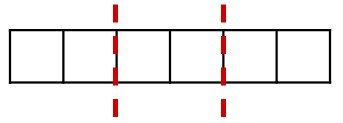
i/iii will exist one of these three equal parts:

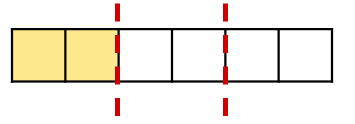
1/3 = 2/6

At present to decrease ane/3 from five/6, we will take away 2 parts from the five parts of the same whole.

v/6 – 1/iii = 5/6 – ii/6 = iii/6

two. Adding/subtracting numerators while ignoring the denominators

As students struggle to run into fractions as unlike operations, they ofttimes treat them as whole numbers.

12/13 + 7/8 = xix, because 12 + seven = nineteen

12/13 – vii/8 = 5, because 12 – seven = v

The key hither is to make their understanding of fractions concrete, right from the very beginning.

3. Adding/subtracting denominators while ignoring the numerators

Some students add only the denominators and ignore the numerators. They look at the denominators equally two whole numbers and add together/subtract them.

12/13 + 7/eight = 21, considering xiii + 8 = 21

12/xiii – vii/eight = 5, because 13 – eight = v

Interesting Activities for Addition and Subtraction of fractions

Incorporate simple activities similar cutting real-world objects to develop interest and a better grasp of fractions. Activities similar Tic tac toe, BINGO, or matching activities can exist done to make fractions bug more fun.

Fraction in Everyday Life

Parents should encourage talking about fractions with kids in everyday life. Encourage kids to apply fractions in twenty-four hour period-to-24-hour interval tasks like equal division of things, in measurement, or while cooking their favorite new recipes. We tin can as well include fractions while talking near time or the marks kids scored in school!

Talking about fractions evades the fear of it and kids are more likely to savour practicing them.

Games on Fractions

Games encourage students to exercise a lot of questions which they generally don't similar doing otherwise. Check out these fun fraction games at SplashLearn

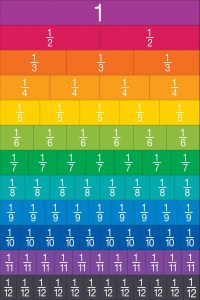
Fractions Models/Manipulatives

Using manipulatives like fraction strips, area models, lego blocks and number lines make fractions interesting and engaging for the kids. These manipulatives aid kids visualize fractions and hence empathize them better.

Fraction Give-and-take bug

Solving contextual problems helps students chronicle fraction learning to real-life situations. They empathise the significance, the need, and importance of fractions and how to apply them to solve issues. You can check out these fraction word problems games on SplashLearn and make fractions a lot simpler!

To Summarize:

It's important for students to recognize that fractions are beyond shading and coloring.
Fractions are numbers that are used to represent the numbers between any two sequent whole numbers.
Assist students practice fractions by cutting, pasting, coloring to help them sympathize fractions better and take fun with them.
Utilize fraction models to help them visualize and grasp addition and subtraction of fractions.
Make sure they know why the steps of adding/subtracting fractions work rather than simply blindly applying the steps.
As a parent,use fractions in everyday conversations, chronicle fractions to real-life contexts and provide them instances from daily life activities like cooking, baking, time and measurement.

Teach Fractions with SplashLearn

Loved by 40+meg parents, SplashLearn is a ane-stop solution for your kids' math and reading journey. You lot can make your picayune learners play games on adding and subtracting fractions or learn through worksheets. With curriculum-aligned didactics, SplashLearn provides a personalized experience that adapts to every kid's needs.

Frequently Asked Questions (FAQs)

1. What are fractions?

Fractions are numbers betwixt the whole numbers (0,1,2,iii,4). They represent a portion/function of an entire affair. A fraction has ii parts – numerator and denominator.

2. What are the steps for calculation and subtracting fractions?

Step 1: Brand denominators the same
Step 2: Add together/Subtract the numerators (keeping the denominator every bit same)
Pace iii: Simplify the fraction

iii. How do you add and subtract fractions with dissimilar denominators?

Fractions with different denominators can be added past converting them to fractions with the same denominators with the assist of equivalent fractions.

4. How do you add and decrease mixed numbers?

First, write the mixed numbers every bit fractions. Now add/subtract but similar you lot do with fractions. In the end, don't forget to convert the answer (fraction) to a mixed number!

five. How do you add and subtract negative fractions?

Negative fractions tin exist considered as fractions with numerators as negative. The steps to add together and decrease the negative fractions remain the aforementioned as fractions except now kids would need to add together negative or positive numerators.